解锁开方运算的精髓：详细教程与实例演示助你轻松掌握

从困惑到上手的真实心得

我一直觉得开方这东西挺玄乎的，小时候第一次在数学课本上看到√9=3，脑子里冒出的第一个问题是：为什么不是别的数？为什么偏偏是3？老师总说“平方的反向操作”，可我那会儿连平方都还半懂不懂呢，后来慢慢发现，开方其实没那么神秘，它就像是数学里的“侦探游戏”——给你结果，让你倒推原因，今天我就结合自己的摸索过程，聊聊怎么拆解开方运算,顺便分享几个踩坑案例。

先别急着背公式！理解“开方到底在干嘛”

很多人一上来就背√2≈1.414，但如果不明白为什么，迟早会忘，我的理解是：开方就是找一个数，让它和自己相乘后等于目标值，25，其实就是问“哪个数乘以自己等于25”？答案5就像藏在迷雾里的线索,你得一步步逼近它。

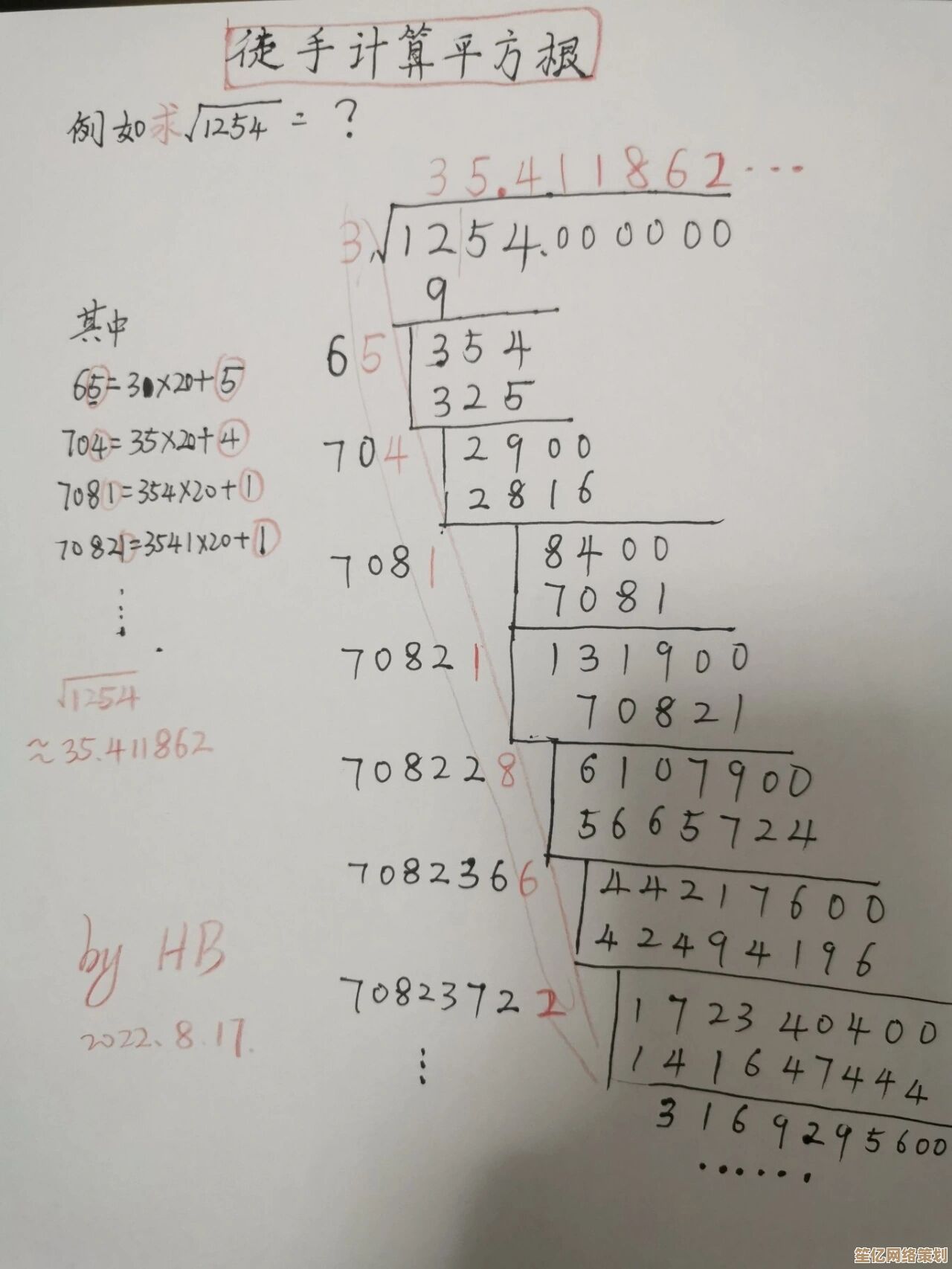
记得高中时我试图手算√2，吭哧吭哧用了“试错法”：1.4×1.4=1.96（太小），1.5×1.5=2.25（太大），然后卡在中间纠结了半天，后来才知道，古人用迭代法（比如巴比伦算法）就能搞定——先猜个大概，再用公式反复优化猜测，比如从1.4开始：

• 第一步：(1.4 + 2/1.4)/2 ≈ (1.4 + 1.428)/2 ≈ 1.414 看，两步就接近了！这种“猜了改，改了再猜”的思路,比硬背有趣多了。

实战案例：从整数的到小数的，别怕麻烦

案例1：√196
乍一看数字挺大，但如果你记得平方数规律（比如14²=196），瞬间就能解锁，关键是多积累常见平方数：11²=121, 12²=144… 我习惯用手机便记记录这些，偶尔瞟一眼,慢慢就熟了。

案例2：√0.09
这是我当年踩过的坑——总觉得小数开方会更复杂，其实本质一样：哪个数乘以自己等于0.09？答案是0.3（因为0.3×0.3=0.09），如果遇到√0.008这类，可以转化成分数：√(8/1000)=√8/√1000≈2.828/31.62≈0.089（这里我用了估算，因为精确算要处理无理数，日常中够用就行）。

案例3：√50的化简
50不是完全平方数，但可以拆成25×2，50=√25×√2=5√2，这种分解思维超实用！比如做设计时计算比例，直接留√2形式反而更准确,不必硬算成小数。

那些“不完美”的思考：开方也有无奈的时候

不是所有开方都能整整齐齐，像√3、√5这类无理数，我至今背不全小数点后十位（虽然考试逼我背过1.732和2.236），但生活中其实没必要纠结精度——做木工裁木板时，我直接用卷尺量个大概；做烘焙按配方√2倍缩放，四舍五入到克就够了，数学的严谨和现实的灵活,得分开看。

还有一次帮邻居算地块面积，√678这样的数冒出来，我干脆用估算：25²=625，26²=676，678≈26.0x（因为678-676=2，微调一丢丢），邻居夸我“算得快”,其实只是偷懒用了近似法而已。

工具和心算的平衡：别死磕

现在手机一点就能开方，但理解原理是为了应对没网络的场合（比如野外露营算距离），我习惯先心算个范围，再用工具验证，120，知道11²=121，所以答案比11小一点点——这种直觉比硬算更重要。

最后想说，开方不是数学家的专利，它藏在生活角落：圆桌的半径、屏幕对角线、甚至咖啡里糖分的配比……偶尔用笔算一算，就像解谜一样好玩，哪怕步骤乱糟糟、草稿纸涂改得像抽象画，那种“啊哈，原来是你！”的瞬间,才是数学真正的魅力。

（完）