用SPSS怎么搞正态分布验证，数据库里数据到底符不符合正态啊

我们通常说的“用SPSS检验正态性”，并不是要得到一个简单的“是”或“否”的答案，而是通过多种方法综合判断数据接近正态分布的程度，因为在实际研究中，尤其是社会科学领域，数据完全服从完美的正态分布几乎是不可能的，我们的目标是判断数据的偏离程度是否严重到会影响我们后续使用的统计方法（比如t检验、方差分析等）。

第一步：最直观的方法——看图说话

在分析数据之前，先画个图来看是最直接的方式,SPSS提供了两种非常常用的图形。

1. 直方图：

   • 操作：在SPSS菜单栏点击“图形” -> “旧对话框” -> “直方图”，将你想检验的变量选入“变量”框，并且一定要勾选右下角的“显示正态曲线”。
   • 怎么看：系统会画出一个条形图（直方图），并在上面叠加一条光滑的钟形曲线（正态曲线），你只需要直观地对比一下，你的数据形成的条形轮廓，是不是跟那条钟形曲线大致吻合，如果轮廓的形状、高峰的位置都跟正态曲线差不多，那就可以初步认为数据近似正态分布，如果形状歪七扭八，或者高峰严重偏向一边,那就不太像正态分布。

2. Q-Q图（分位数-分位数图）：

   • 操作：在菜单栏点击“分析” -> “描述统计” -> “Q-Q图”，将变量选入“变量”列表,其他设置通常保持默认即可。
   • 怎么看：这个图会画出一个个散点，如果数据完全服从正态分布，这些点应该紧紧地排成一条从左下到右上的直线，你的主要任务就是看这些点是不是大致在一条直线上，如果点的分布和直线高度重合，那就很好；如果点严重偏离直线，尤其是在两端（图的左上角和右下角）偏离很大,那就说明数据的分布和正态分布有差异。

第二步：看数字指标——更精确的判断

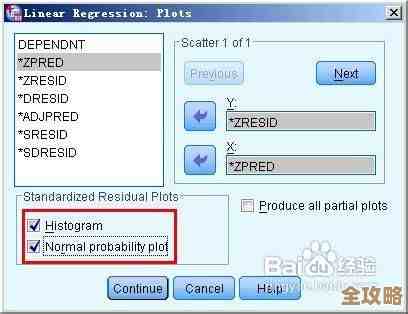
图形虽然直观，但有时候会因人而异，不够客观，这时候就需要看具体的统计检验指标，SPSS的“描述统计”功能能提供关键数值。

• 操作：点击“分析” -> “描述统计” -> “描述”，将变量选入“变量框”，然后点击右上角的“选项”按钮，确保勾选了“偏度”和“峰度”，点击“继续”和“确定”运行。

运行后，你会得到一个表格，里面有两个非常重要的指标：偏度 和 峰度。

• 偏度：衡量数据分布对称性的指标。

  • 理想值：0，表示分布完全对称,像标准的钟形一样。
  • 正值：大于0，表示数据中有较多较大的值，图形的高峰会向左偏，右边拖着一条长尾巴（正偏态或右偏态），分析个人收入，少数人收入极高,就会导致右偏。
  • 负值：小于0，表示数据中有较多较小的值，高峰向右偏，左边拖着长尾巴（负偏态或左偏态）。
  • 判断标准：一个经验法则是，当偏度的绝对值小于2时，可以认为偏斜程度尚可接受，近似对称，如果绝对值大于2,则偏离就比较严重了。

• 峰度：衡量数据分布陡峭程度的指标。

  • 理想值：0（SPSS通常以正态分布的峰度为0作为基准）。
  • 正值：大于0，表示分布形态比标准正态分布更陡峭、更高瘦，尾部更厚（尖峰态）。
  • 负值：小于0，表示分布形态比标准正态分布更扁平、更矮胖，尾部更薄（平峰态）。
  • 判断标准：同样，峰度的绝对值小于2时,通常认为峰度的问题不大。

第三步：正式的统计检验——柯尔莫戈洛夫-斯米尔诺夫检验和夏皮洛-威尔克检验

这是两种专门用于正态性检验的假设检验方法。

• 操作：点击“分析” -> “描述统计” -> “探索”，将待检验变量选入“因变量列表”，然后点击右边的“图”按钮，在新对话框中，勾选“含检验的正态图”，点击“继续”和“确定”。

  

• 怎么看结果：在输出结果中，你会看到“正态性检验”表格，这个表里就有K-S检验和S-W检验的结果，你需要重点关注 “显著性” 这一列。

  • 原假设：检验的原假设是“数据服从正态分布”。
  • 判断标准：如果显著性（Sig.值）大于0.05，说明没有足够的证据拒绝原假设，即认为数据服从正态分布，如果显著性小于0.05，则拒绝原假设，认为数据不服从正态分布。

• 注意：当样本量很大时（比如超过2000），K-S检验非常敏感，即使数据只是轻微偏离正态，它也可能得出显著（即不服从正态）的结果，对于大样本，更推荐使用S-W检验的结果,或者重点参考前面的图形和偏度峰度指标。

综合判断：数据库里的数据到底符不符合正态啊？

现在回到你的核心问题，你不能只依赖某一个方法就下结论,需要综合判断：

1. 先看图：直方图和Q-Q图看起来是不是大致正常？如果图形看起来已经明显畸形了,那基本可以断定不是正态分布。
2. 再看数：偏度和峰度的绝对值是否都小于2？如果是,加分。
3. 最后看检验：S-W检验的Sig.值是否大于0.05？如果是,加分。

最终结论通常是这样表述：

• 符合正态分布：图形大致吻合，偏度峰度绝对值均小于2，且S-W检验p值>0.05。
• 轻微偏离正态但可接受：图形略有偏差，但偏度峰度绝对值在2-3之间，S-W检验p值可能略小于0.05（尤其在样本量较大时），对于许多统计方法（如t检验、方差分析）这种程度的偏离被认为是“稳健”的，即影响不大,可以当作近似正态来处理。
• 严重偏离正态：图形严重畸形，偏度或峰度绝对值很大（比如超过3），S-W检验p值远小于0.05，这种情况下，你可能需要考虑使用非参数检验（如曼-惠特尼U检验代替t检验）或者对数据进行转换（如取对数）来改善正态性。

正态性检验是为你的研究目的服务的，关键是判断偏离是否会影响你下一步要做的分析，而不是追求一个100%完美的正态分布。