解密各类平面图形面积求解策略：高效学习几何知识必备手册

📐 解密各类平面图形面积求解策略：我的几何血泪史

几何这东西吧，说难不难，说简单吧…有时候真想把手里的圆规扎进课本里😅，但面积计算绝对是几何里的"生存必备技能"，今天就来聊聊我这些年踩过的坑和悟出的门道——绝对不教科书！

1️⃣ 矩形/正方形：你以为你会？

"长×宽"三岁小孩都会背？但上次帮表弟辅导作业，题目是："用篱笆围一个面积最大的长方形菜地，篱笆总长20米"，这小子直接画了个5×5的正方形…错！ 实际上当周长固定时，正方形确实是面积最大的矩形（这个结论可以用二次函数证明，但当时我只会暴躁地翻白眼🙄）。

个人骚操作：遇到不规则四边形，我习惯用对角线切成两个三角形，毕竟…三角形面积公式我闭着眼都能背（后面会说到这个梗）。

2️⃣ 三角形：我的初恋与噩梦

"底×高÷2"这个公式我小学就会，直到初中遇到钝角三角形才翻车——原来"高"可以跑到三角形外面！😱 当时我的作业本上全是涂改液痕迹…

血泪案例：已知三角形三边长为5、7、8，用海伦公式：

1. 先算半周长 s=(5+7+8)/2=10
2. 面积=√[10×(10-5)×(10-7)×(10-8)]=√(10×5×3×2)=√300≈17.32

（突然想到当年因为漏写平方根符号被扣分，现在手心还会冒汗💦）

3️⃣ 圆形：π的阴谋

S=πr² 这个公式让我产生过世纪疑问：为什么是r的平方不是立方？后来看阿基米德用"化圆为方"的极限思想推导才懂…虽然考试不考证明，但这种理解让我再也没混淆过球体表面积公式（4πr²，别问我怎么记住的，说多了都是泪）。

实战技巧：遇到"半个圆+矩形"的组合图形，我总先算整圆面积再除以2，比直接算半圆少出错（别问我怎么知道的🤡）。

4️⃣ 梯形：被低估的王者

"(上底+下底)×高÷2"这个公式我编了个重口味口诀："两个底相加，乘高像戴帽，最后除以2，谁也跑不掉"（当年在课本角落写的，现在看简直羞耻到脚趾抠地…）。

惊人发现：任何四边形只要两组对边中有一组平行，就能当梯形算！比如那个让我挂科的变态题："直角梯形斜腰延长线与上底延长线围成的区域面积"…算了不想回忆了😇。

5️⃣ 不规则图形：我的野路子

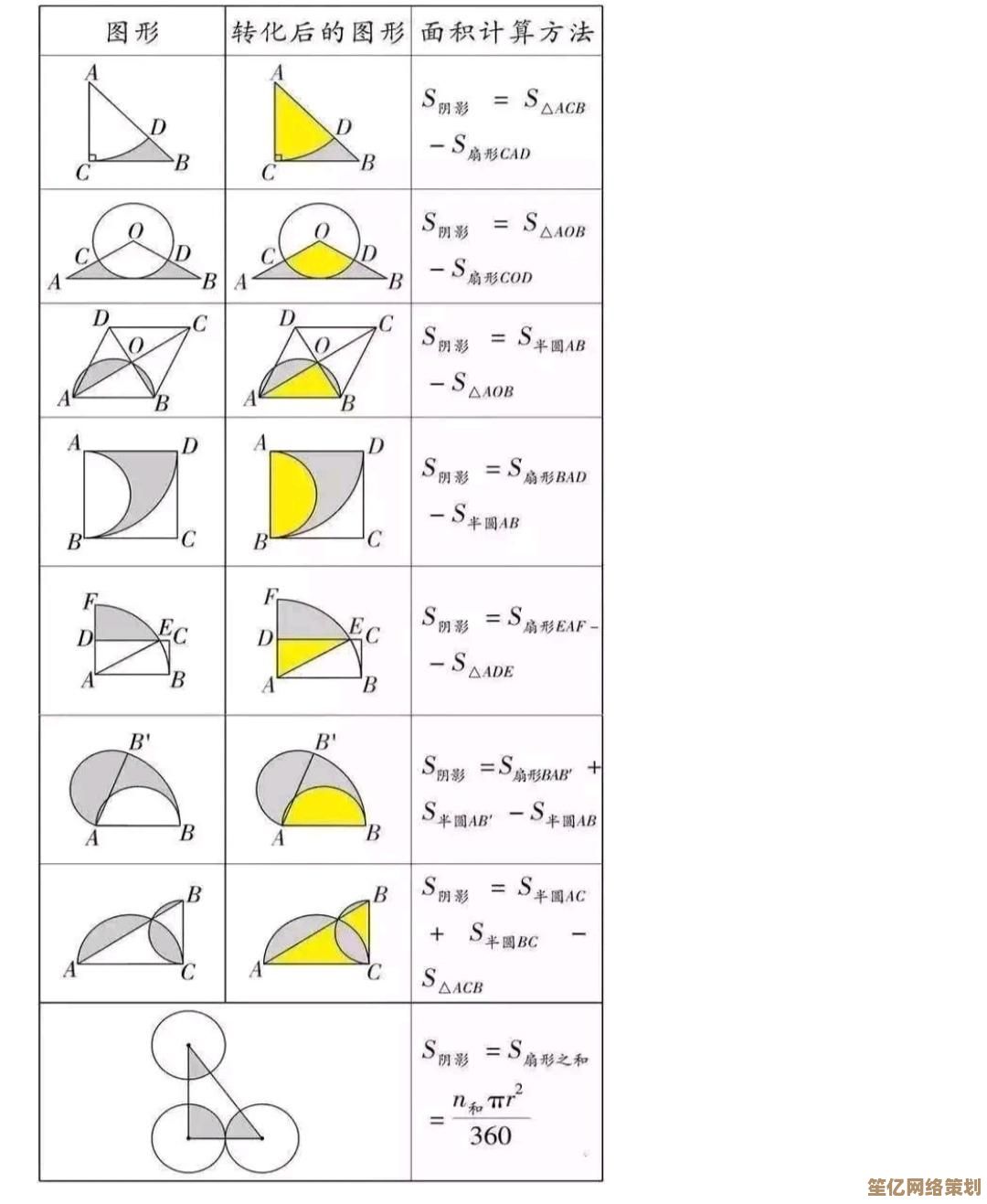
遇到数学课本最后那种妖魔鬼怪图形，我的必杀技是：

1. 切成三角形+矩形+半圆等基本图形（像玩拼图🧩）
2. 用坐标法（适合有坐标系时）
3. 撒把米用蒙特卡洛方法（划掉）

有次考试遇到"花瓣形"面积，我直接用圆面积减去内接正方形面积…结果当然错了，但老师给了步骤分！所以啊，写错公式也比空白强✍️。

💡 我的暴论时间

• 背公式不如懂公式怎么来的（比如三角形面积公式其实就是半个平行四边形）
• 考试时先写公式再代入数字！有次我数字全对但忘了写÷2，直接50分变25分…
• 量纲检查法：面积单位肯定是平方，如果算出"米"那绝对错了（别笑，我真干过）

现在看到几何题已经不会胃痛了，甚至有点享受那种"拆解-重组"的过程…虽然偶尔还是会犯把直径当半径的低级错误啦😝，你呢？最怕遇到哪种图形？