数独迷快来，这些同类数字游戏能停不下来.

数独迷快来，这些同类数字游戏能停不下来... 引自“果壳”、“知乎”用户分享及“经典谜题游戏合集”等综合资料）

数独的魅力，只有沉浸其中的人才能体会，那种在九宫格间抽丝剥茧，最终让所有数字各归其位的成就感，实在让人上瘾，但如果你已经把标准数独玩得滚瓜烂熟，正在寻找新的挑战，或者你是个新手想找些不一样的开胃菜，那么恭喜你，数字逻辑游戏的海洋广阔无垠，有太多同样迷人、甚至更烧脑的同类游戏在等着你，它们有的规则略有变化，有的思路截然不同，但核心的乐趣——那种基于逻辑推理的纯粹快乐——是相通的。

如果你爱数独，那么从它的近亲开始尝试是最顺理成章的，杀手数独”，这是数独一个非常受欢迎的变体，它同样是在9x9的格子中填入1-9，并且满足每行、每列、每个3x3宫的数字不重复，但它的最大不同在于，盘面上没有了那些给定的初始数字，取而代之的是一些用虚线框起来的“笼子”，每个笼子角落会有一个小数字，那是该笼子内所有数字之和，你得同时满足“不重复”和“求和”这两个条件，这就像在解数独的同时，又融入了简易数独的乐趣，挑战性瞬间提升，你需要更灵活地运用数字间的组合关系，推理的层次也更加丰富，知乎上有玩家分享说，从标准数独转向杀手数独，就像从平地跑步升级成了障碍跑，虽然更累,但乐趣也倍增。

除了杀手数独，还有“对角线数独”，它在标准规则的基础上，增加了一条甚至两条大对角线上的数字也不能重复的规则，这小小的改动，却极大地改变了盘面的约束条件，很多时候能提供关键的唯一解线索,让你的解题策略需要随之调整。

如果你觉得这些变化还不够刺激，想尝试一些规则完全不同但逻辑内核相似的“远亲”，那选择就更多了，首推的可能是“数壹”，也常被称为“数和”，这个游戏和数独看起来完全不同，它是在一个空白网格中进行的，网格中有一些带数字的圆圈，这些圆圈位于格子之间的交叉点上，规则是：从每个带数字的圆圈出发，画一条直线（横或竖），直线的长度（即穿过的格子数）正好等于圆圈内的数字，所有的直线不能交叉或连接，最终要填满整个网格，数壹的乐趣在于，它更像是在网格上进行几何构图，你需要从那些给定的数字（尤其是角落和边缘的数字）开始，一步步推理出线条的走向，非常考验空间想象和逻辑排除能力，果壳曾有一篇文章专门介绍数壹，称其为“安静的逻辑风暴”,一旦开始就停不下来。

另一个不得不提的是“数墙”，也叫“岛”，游戏盘面也是网格，网格中有一些带数字的格子，你的任务是用横向或纵向的墙壁将网格划分成若干个区域，每个区域内恰好包含一个带数字的格子，并且这个数字代表了该区域所占的格子数，所有区域必须连成一片（不能有孤立的小岛），墙壁也不能形成2x2或更大的闭合空心方块，数墙的解题过程就像是在创建一个群岛地图，你需要反复推敲墙壁的摆放位置，确保每个“岛屿”的大小刚刚好，它结合了划分和计数的乐趣,逻辑链条非常独特。

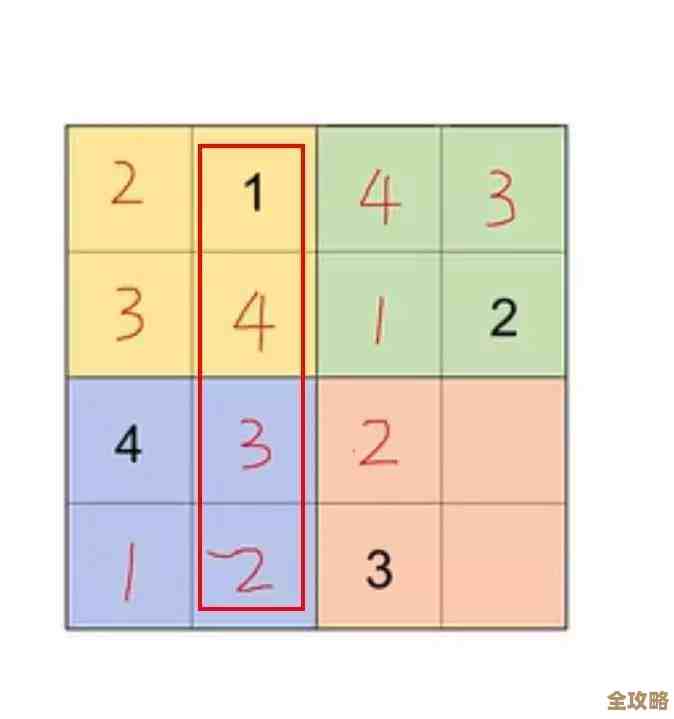
对于喜欢算术的玩家，“肯肯”是一个绝佳的选择，它的盘面是一个简单的方阵，被粗线划分成若干个不规则区域（称为“笼”），规则是：在空格中填入数字（通常是1到方阵的阶数，如4x4格填1-4，6x6格填1-6），使得每一行、每一列的数字都不重复，每个“笼”的左上角会有一个数字和一个运算符号（如+、-、×、÷），这意味着该笼内所有数字经过指定运算后，必须得到那个目标数字，一个两格笼标着“5+”，意味着里面的两个数字相加等于5，那么只能是2和3，肯肯将数独的排列要求与基础算术完美结合，你需要同时进行逻辑推理和数字分解，对大脑是双重的锻炼，很多经典谜题游戏合集中都会包含肯肯,它被认为是培养数学思维的优秀工具。

如果你追求极致的简洁和深邃，可以试试“二进制数独”，也就是“Binary Puzzle”，它通常在一个矩形网格中进行，里面只有两种符号，比如0和1，规则很简单：每行每列中，0和1的数量相等（对于偶数尺寸网格），不能有连续三个或以上相同的数字出现（不能有“111”或“000”这样的情况），并且所有行和列都必须是独一无二的，别看规则简单，解起来却异常烧脑，你需要运用简单的规则推导出极其复杂的局面，每一步都需要深思熟虑,非常适合喜欢抽象思考的玩家。

数字逻辑游戏的世界远不止数独一种，无论是它的变体杀手数独、对角线数独，还是风格迥异的数壹、数墙、肯肯和二进制谜题，它们都共享着同一个灵魂：用清晰的规则，构建起一个充满挑战的谜题空间，让玩家依靠纯粹的推理能力一步步走向终点，这种在约束条件下寻找唯一通路的乐趣，正是它们让人停不下来的根本原因，数独迷们，大胆地去探索这些新大陆吧，你会发现，逻辑的乐趣,没有边界。