探索绝对值函数揭示数学世界的精确性与美学魅力

当数学脱下它的完美外衣

我小时候一直觉得数学是个冷酷的完美主义者，直到我遇见了绝对值函数，它看起来简单——一个“V”字形，像折纸一样干脆利落，但真正玩起来，才发现它藏着不少狡猾的小把戏。

绝对值的“双面人格”

绝对值函数的定义简单到让人掉以轻心：
[ |x| = \begin{cases} x & \text{} x \geq 0 \ -x & \text{} x < 0 \end{cases} ]

但就是这个“非负即反”的逻辑，让它在数学里像个精明的谈判专家，解方程 (|x - 3| = 5)，它不会直接告诉你答案，而是狡猾地拆成两个可能：

• (x - 3 = 5) → (x = 8)
• 或者 (x - 3 = -5) → (x = -2)

你看，它早就准备好了两个答案，却假装自己是个单纯的直线函数。😏

当绝对值遇上现实：误差的温柔面具

数学老师总说绝对值代表“距离”，但我觉得它更像是一种“温柔的纠正”，测量误差时，我们不在乎偏差是正还是负，只关心“差了多少”，绝对值在这里扮演了一个公平的裁判，把一切负面的东西（负误差）都变成正面的考量。

这让我想到生活里的一些事——我们太在意方向（正负），却忽略了“距离”本身的意义，绝对值教会我们：重要的不是你在哪边，而是你走了多远。 🤔

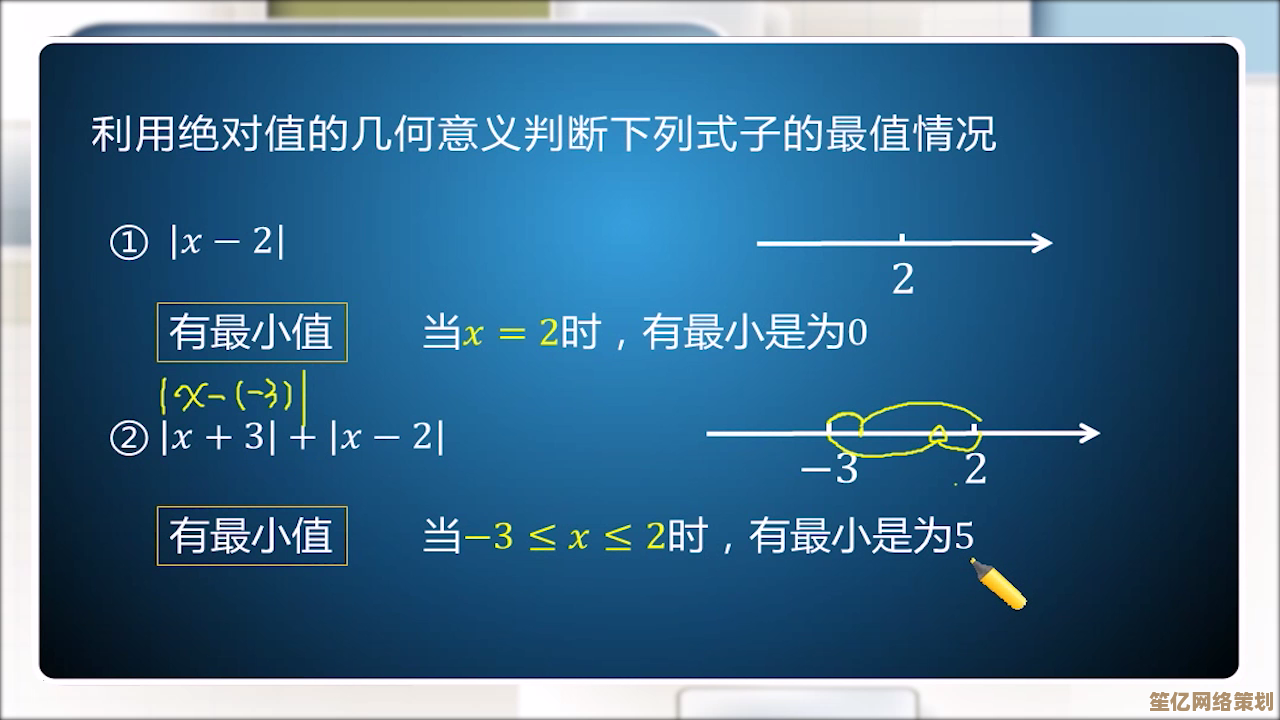
绝对值的“美学暴击”

画绝对值函数的图像时，我总会被它的对称美震撼，它像一座山峰，也像折翼的鸟突然振翅，而当你叠加多个绝对值函数，(y = |x| + |x - 2|)，它会形成更复杂的折线，像阶梯，又像锯齿状的闪电。⚡

有一次，我试着画 (y = ||x| - 1|)，结果得到了一个“W”形——数学竟然在跟我玩俄罗斯套娃！这种层层嵌套的绝对值的游戏，让我突然意识到，数学的“精确”背后，其实藏着不少幽默感。

不完美的思考：绝对值会“说谎”吗？

绝对值有个“缺点”——它掩盖了原始数据的符号。(-5) 和 (5) 的绝对值都是 (5)，但它们的意义完全不同，在统计学里，这可能导致误判，就像生活中，如果我们只看“努力的程度”而不管方向，可能会南辕北辙。

绝对值是精确的，但精确≠全面，它像一面镜子，却只反射大小，不反射正反，这算不算数学的一种“美丽的局限”？

数学的“不完美”魅力

绝对值函数让我明白，数学不是冷冰冰的规则，而是一场充满意外的探险，它精确，但也狡猾；它简洁，但也复杂，或许，正是这种“不完美”，才让数学有了人的温度。

下次再看到 (|x|)，别只把它当工具——试试和它玩个游戏，看看它能带你发现什么。🎲