探秘四舍五入函数:专业方法与高效技巧深度解析
- 问答
- 2025-10-28 02:44:57
- 32
根据微软官方支持文档和通用编程知识,四舍五入是数学计算中一个基础但至关重要的操作,它不仅仅是简单的“遇5则进”,背后有多种规则和适用场景。
四舍五入的核心规则与常见误区
最常见的四舍五入规则是“四舍五入,五成双”,也叫“银行家舍入法”或“向偶数舍入”,很多人误以为看到5就无条件进位,但专业方法更复杂。
- 基本规则(四舍五入,五成双):当需要舍去部分的首位数字小于5时,直接舍去(四舍);当首位数字大于5时,进位(六入),关键在于当首位数字等于5,且5后面没有其他非零数字时,要看被保留部分的末位数字:如果是奇数则进位,如果是偶数则舍去,这样做的目的是在大量统计计算中,使舍入误差相互抵消,结果更精确。
- 例子(保留1位小数):
24->2(4小于5,直接舍去)26->3(6大于5,进位)25->2(5后面无数字,前一位是偶数2,所以舍去)35->4(5后面无数字,前一位是奇数3,所以进位)251->3(5后面有数字1,属于大于5的情况,因此进位)
- 例子(保留1位小数):
Excel中的四舍五入函数家族
根据微软Office支持网站,Excel提供了一系列函数来处理不同的舍入需求。
-
ROUND函数(标准四舍五入)
- 功能:最常用的函数,严格遵循“四舍五入,五成双”的银行家舍入法则。
- 语法:
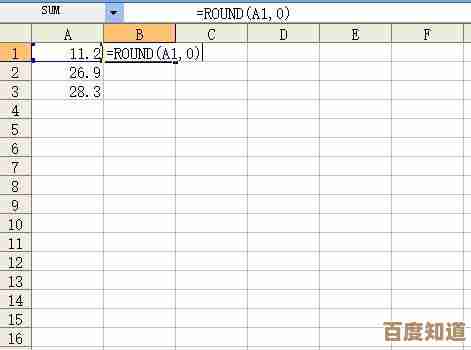
=ROUND(数字, 小数位数) - 例子:
=ROUND(2.15, 1)结果为2(5前面是奇数1,进位)=ROUND(2.25, 1)结果为2(5前面是偶数2,舍去)=ROUND(12.349, 2)结果为35(第三位9大于5,第二位4进位成5)
-
ROUNDUP函数(向上舍入)
- 功能:无论数字大小,总是向绝对值更大的方向舍入,可以理解为“有小数就进一”。
- 语法:
=ROUNDUP(数字, 小数位数) - 例子:
=ROUNDUP(3.14159, 2)结果为15=ROUNDUP(-3.14159, 1)结果为-3.2=ROUNDUP(5, 0)结果仍为5
-
ROUNDDOWN函数(向下舍入)
- 功能:与ROUNDUP相反,总是向绝对值更小的方向舍入,直接截断指定位数后的数字。
- 语法:
=ROUNDDOWN(数字, 小数位数) - 例子:
=ROUNDDOWN(3.14159, 2)结果为14=ROUNDDOWN(-3.14159, 1)结果为-3.1=ROUNDDOWN(19.99, 0)结果为19
-
MROUND函数(按倍数舍入)
- 功能:返回一个按指定倍数舍入后的数字,它遵循“四舍五入”原则,但目标是最近的指定基数的倍数。
- 语法:
=MROUND(数字, 倍数) - 例子:
=MROUND(10, 3)结果为9(因为10离9比离12更近)=MROUND(15, 6)结果为18(15正好在12和18中间,函数会向上舍入到18)- 包装场景:产品单价1.5元,客户买7个,
=MROUND(7, 6)可以计算需要按6个一盒包装,结果是6盒(但实际计算总价通常用不到,这里举例说明倍数概念)。
高效技巧与场景应用
- 财务计算:计算金额时,法律规定通常精确到分(两位小数),必须使用
ROUND函数在每一步计算后对结果进行舍入,避免“分币误差”累积成大的账面错误。 - 库存与包装:需要将物品数量按固定包装规格(如每箱12瓶)进行舍入时,
MROUND函数非常实用,计算53瓶水需要多少箱:=MROUND(53, 12)得到60(即5箱),但更常用的可能是计算需要几箱(用ROUNDUP):=ROUNDUP(53/12, 0)得到5。 - 避免浮点误差:计算机处理小数时有精度限制,可能导致像
1+0.2不等于3的情况,在需要精确比较或显示时,先用ROUND函数将结果舍入到合理位数。 - 结合其他函数:舍入函数可以嵌套在其他公式中,先用SUM求和,再对和进行舍入:
=ROUND(SUM(A1:A10), 2)。
重要提醒:不要使用单元格的“格式化”功能来显示小数位数达到舍入目的,格式化只改变显示效果,实际参与计算的仍是原始长小数,真正的舍入必须使用函数来改变存储的数值本身。
本文由黎家于2025-10-28发表在笙亿网络策划,如有疑问,请联系我们。
本文链接:http://waw.haoid.cn/wenda/49045.html